Klassikal fysiks

Klassikal fysiks bi a grup of fysiks theoris wey predayt modern, moh komplit, or moh waidly applikabul theoris. If a korrently asepted theori dé konsidad to bi modern, and e introdukshion reprisent a major paradaim shift, then di previous theoris, or niu theoris bayzd on di olda paradaim, ga often dé referd to as belongin to di area of "klassikal fysiks".

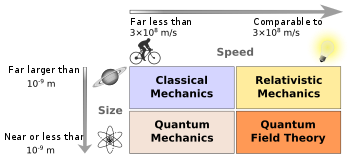
As such, di definishion of a klassikal theori depends on kontex. Klassikal fysikal konsepts often dé yuzd wen modern theoris unnecessarily de komplex for a partikula situashion. Most often, klassikal fysiks refers to pre-1900 fysiks, while modern fysiks refers to post-1900 fysiks, which inkorporayts elements of quantum mekaniks and relativity.^[1]

Ovaview

Klassikal theori get at least tuw distinkt meanings for fysiks. For di kontex of quantum mekaniks, klassikal theori refer to theoris of fysiks wey no dé yuz di quantizashion paradaim, which inklud klassikal mekaniks and relativity.^[2] Laikwaiz, klassikal field theoris, such as jeneral relativity and klassikal elektromagnetisim, bi those wey no dé yuz quantum mekaniks.^[3] For di kontex of jeneral and special relativity, klassikal theoris bi those wey dé obey Galilean relativity.^[4]

Dependin on point of view, among di branches of theori wey dé somtaims inkluded for klassikal fysiks variably bi:

Klassical mekaniks
- Newton's laws of moshion
- Klassikal Lagrangian and Hamiltonian formalisims
Klassikal elektrodynamiks (Maxwell Equashions)
Klassikal thermodynamiks
Klassikal kaios theori and nonlinia dynamiks

Also see

Referens

↑ Weidner and Sells, Elementary Modern Fysiks Prefais p.iii, 1968
↑ Morin, David (2008). Introdukshion to Klassikal Mekaniks. New York: Cambridge University Press. ISBN 9780521876223.
↑ Barut, Asim O. (1980) [1964]. "Introdukshion to Klassikal Mekaniks". Elektrodynamiks and Klassikal Theori of Fields & Partikuls. New York: Dova Poblikashions. ISBN 9780486640389.
↑ Einstein, Albert (2004) [1920]. Relativity. Robert W. Lawson. New York: Barnes & Noble. ISBN 9780760759219.

[1] Weidner and Sells, Elementary Modern Fysiks Prefais p.iii, 1968

[2] Morin, David (2008). Introdukshion to Klassikal Mekaniks. New York: Cambridge University Press. ISBN 9780521876223.

[3] Barut, Asim O. (1980) [1964]. "Introdukshion to Klassikal Mekaniks". Elektrodynamiks and Klassikal Theori of Fields & Partikuls. New York: Dova Poblikashions. ISBN 9780486640389.

[4] Einstein, Albert (2004) [1920]. Relativity. Robert W. Lawson. New York: Barnes & Noble. ISBN 9780760759219.

[1]

[2]

[3]

[4]